ABSTRACT
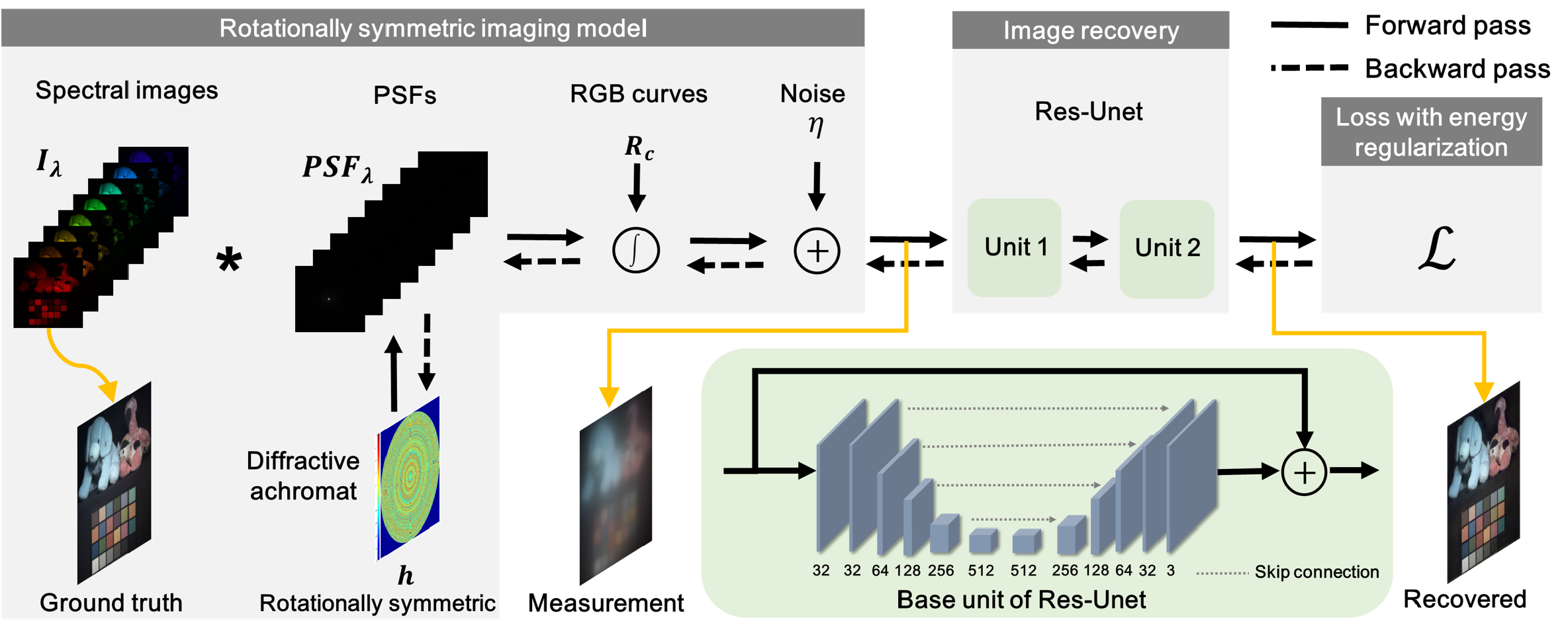
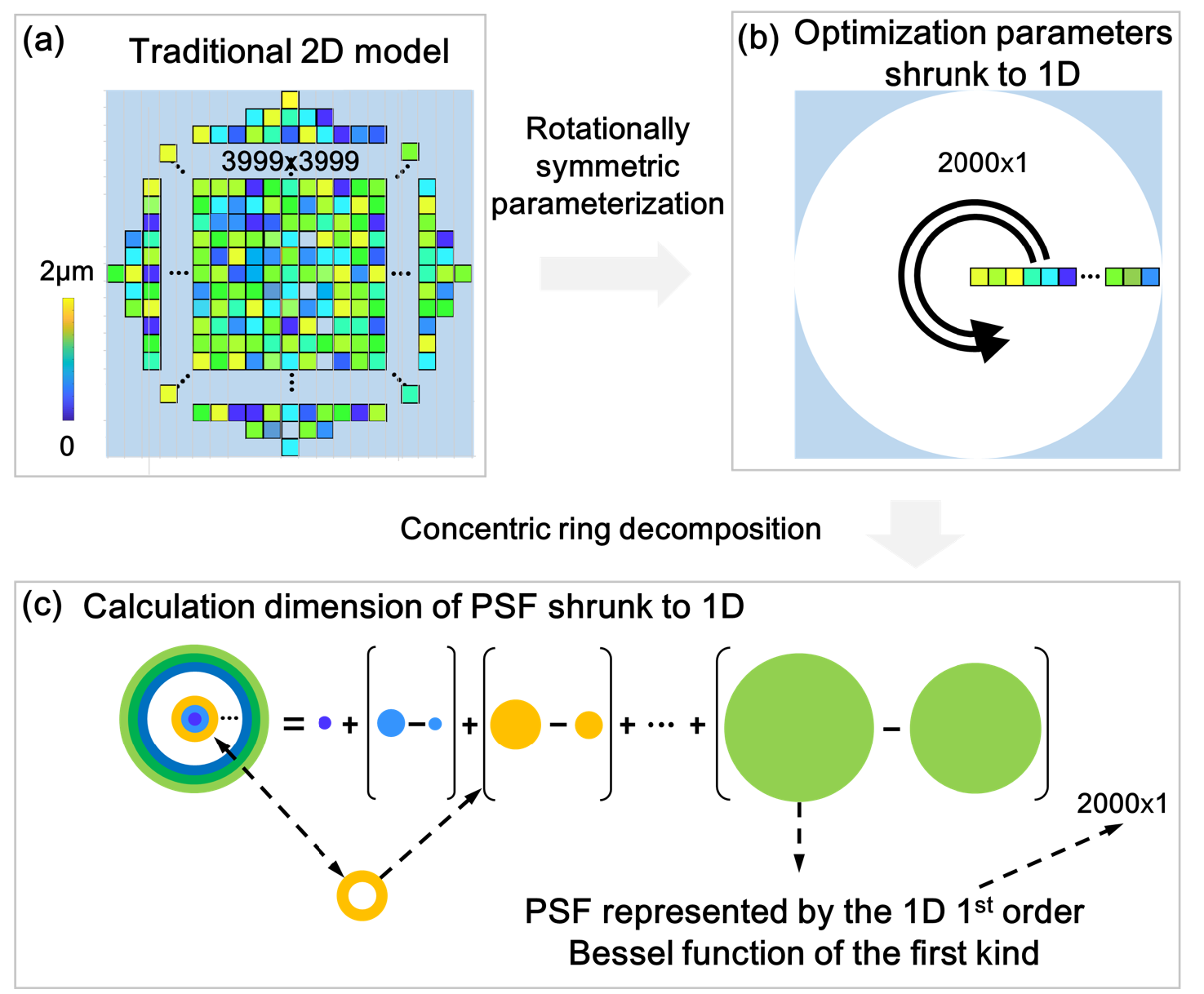
Diffractive achromats (DAs) promise ultra-thin and light-weight form factors for full-color computational imaging systems. However, designing DAs with the optimal optical transfer function (OTF) distribution suitable for image reconstruction algorithms has been a difficult challenge. Emerging end-to-end optimization paradigms of diffractive optics and processing algorithms have achieved impressive results, but these approaches require immense computational resources and solve non-convex inverse problems with millions of parameters. Here, we propose a learned rotational symmetric DA design using a concentric ring decomposition that reduces the computational complexity and memory requirements by one order of magnitude compared with conventional end-to-end optimization procedures, which simplifies the optimization significantly. With this approach, we realize the joint learning of a DA with an aperture size of 8 mm and an image recovery neural network, i.e., Res-Unet, in an end-to-end manner across the full visible spectrum(429–699 nm). The peak signal-to-noise ratio of the recovered images of our learned DA is 1.3 dB higher than that ofDAs designed by conventional sequential approaches. This is because the learned DA exhibits higher amplitudes of theOTF at high frequencies over the full spectrum. We fabricate the learned DA using imprinting lithography. Experiments show that it resolves both fine details and color fidelity of diverse real-world scenes under natural illumination. The proposed design paradigm paves the way for incorporating DAs for thinner, lighter, and more compact full-spectrum imaging systems.