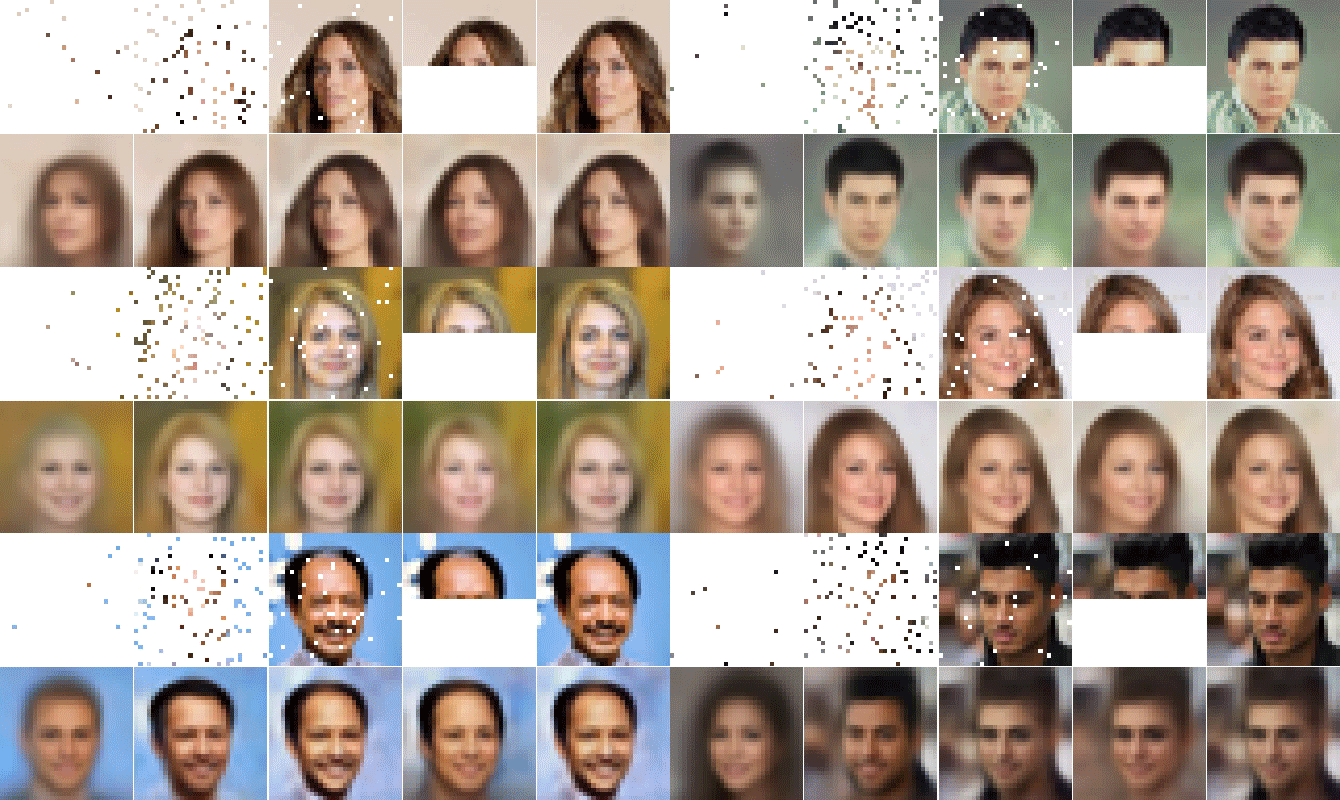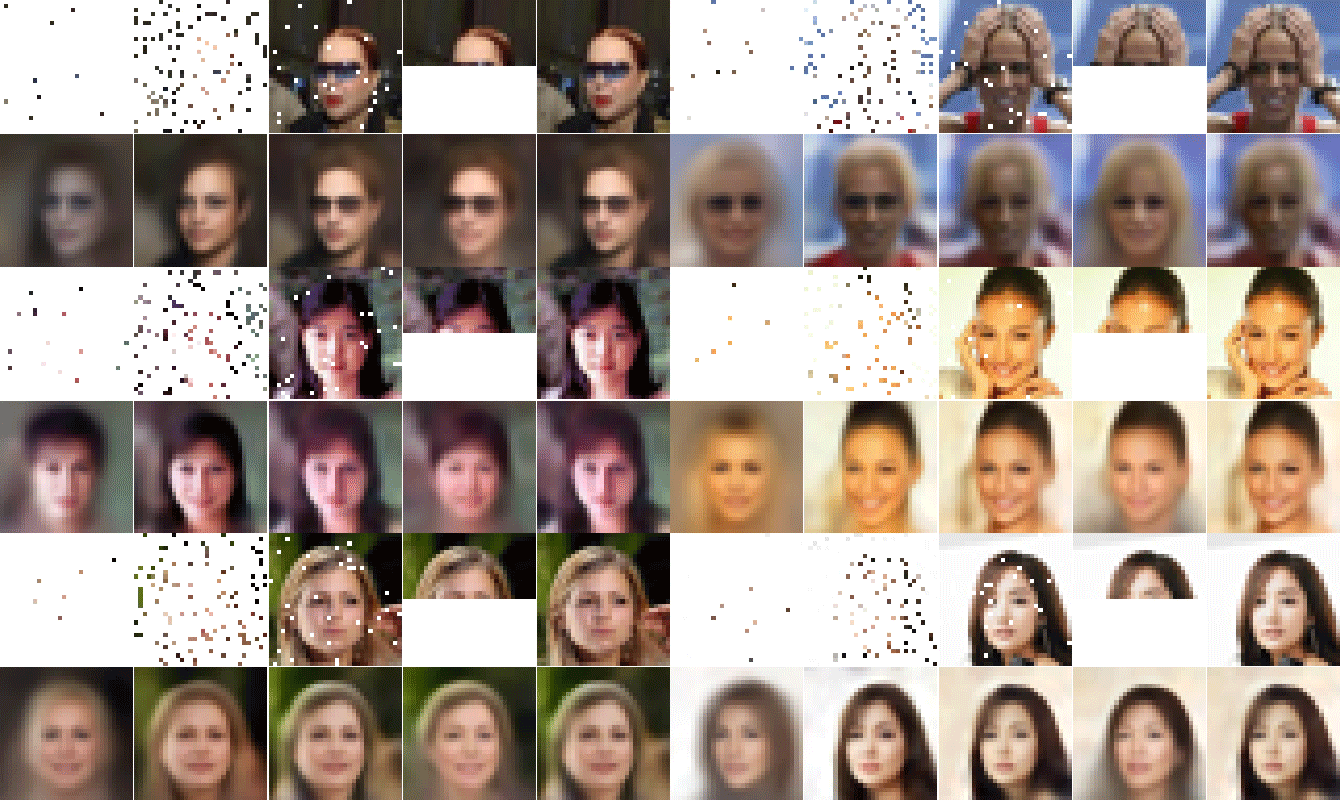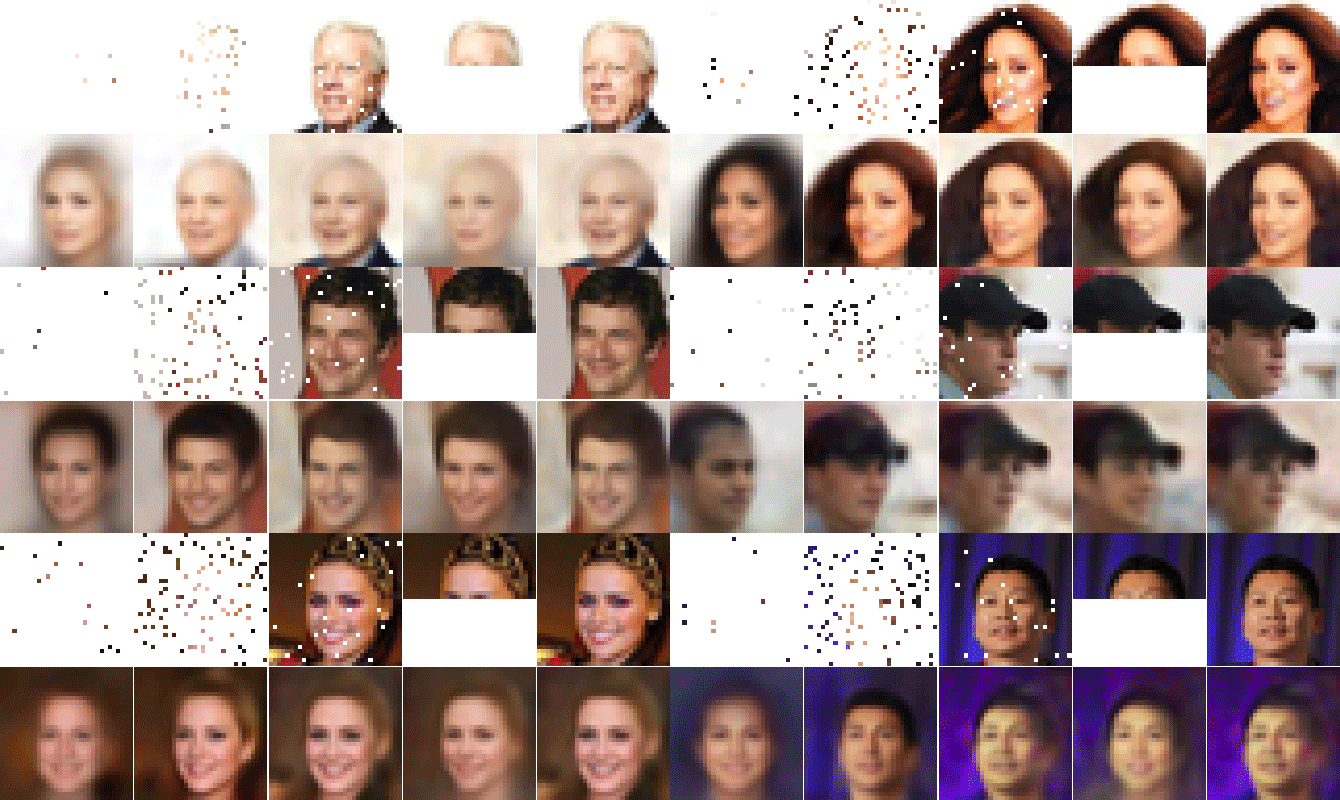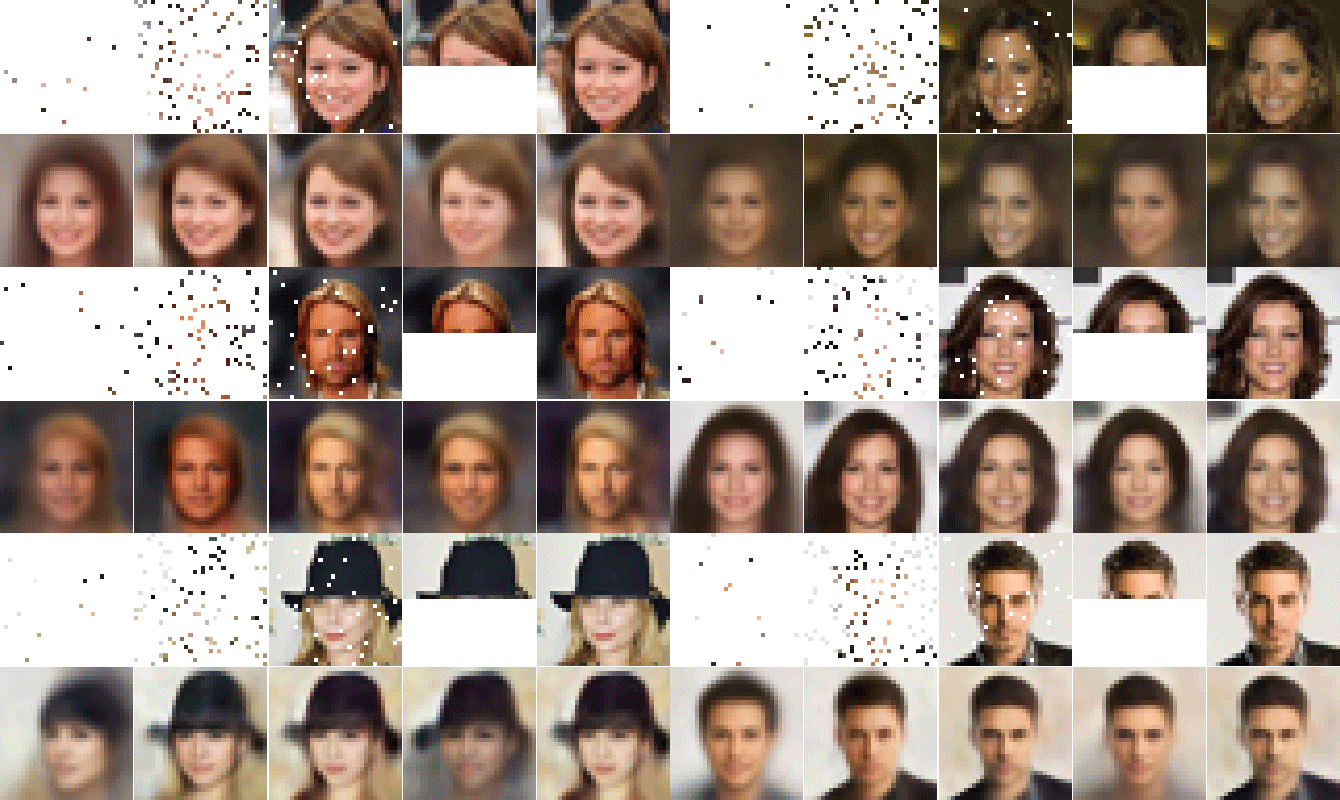Implicit Neural Representations with Periodic Activation Functions | NeurIPS 2020

V. Sitzmann*, J. N. P. Martel*, A. W. Bergman, D. B. Lindell, G. Wetzstein

An implicitly defined neural signal representation for images, audio, shapes, and wavefields.

ABSTRACT

Implicitly defined, continuous, differentiable signal representations parameterized by neural networks have emerged as a powerful paradigm, offering many possible benefits over conventional representations. However, current network architectures for such implicit neural representations are incapable of modeling signals with fine detail, and fail to represent a signal’s spatial and temporal derivatives, despite the fact that these are essential to many physical signals defined implicitly as the solution to partial differential equations. We propose to leverage periodic activation functions for implicit neural representations and demonstrate that these networks, dubbed sinusoidal representation networks or SIREN, are ideally suited for representing complex natural signals and their derivatives. We analyze SIREN activation statistics to propose a principled initialization scheme and demonstrate the representation of images, wavefields, video, sound, and their derivatives. Further, we show how SIRENs can be leveraged to solve challenging boundary value problems, such as particular Eikonal equations (yielding signed distance functions), the Poisson equation, and the Helmholtz and wave equations. Lastly, we combine SIREN with hypernetworks to learn priors over the space of SIREN functions.

FILES

 

CITATION

V. Sitzmann*, J. N. P. Martel*, A. W. Bergman, D. B. Lindell, G. Wetzstein, Implicit Neural Representations with Periodic Activation Functions, Conference on Neural Information Processing Systems (NeurIPS), 2020

@inproceedings{sitzmann2020siren,
author = {Sitzmann, Vincent and Martel, Julien N.P. and Bergman, Alexander W. and Lindell, David B. and Wetzstein, Gordon},
title = {Implicit Neural Representations with Periodic Activation Functions},
booktitle = {Conference on Neural Information Processing Systems (NeurIPS)},
year={2020}
}

A SIREN that maps 2D pixel coordinates to a color may be used to parameterize images. Here, we supervise SIREN directly with ground-truth pixel values. Siren not only fits the image with a 10 dB higher PSNR and in significantly fewer iterations than all baseline architectures, but is also the only MLP that accurately represents the first- and second order derivatives of the image. This video shows the convergence behavior.
A SIREN with pixel coordinates together with a time coordinate can be used to parameterize a video. Here, SIREN is directly supervised with the ground-truth pixel values, and parameterizes video significantly better than a ReLU MLP.
We can recover a signed distance function (SDF) from a point cloud by solving the Eikonal equation. Results achieved by a ReLU MLP are shown on the left and SIREN on the right. Given only the oriented point cloud, SIREN can recover this scene accurately reproducing fine detail in less than an hour of training. In contrast to recent work on combining voxel grids with neural implicit representations, this stores the full scene in the weights of a single, 5-layer neural network, with no 2D or 3D convolutions, and orders of magnitude fewer parameters.
We can recover a signed distance function (SDF) from a point cloud by solving the Eikonal equation. Results achieved by a ReLU MLP are shown on the top and SIREN on the bottom. Given only the oriented point cloud, SIREN can recover this complex scene accurately. In contrast to recent work on combining voxel grids with neural implicit representations, this stores the full scene in the weights of a single, 5-layer neural network, with no 2D or 3D convolutions, and orders of magnitude fewer parameters.
Here, we use SIREN to solve the inhomogeneous Helmholtz equation. ReLU- and Tanh-based architectures fail entirely to converge to a solution. The video shows the convergence behavior.
Generalizing over a space of SIRENs allows us to solve inverse problems, such as image inpaining.

Related Projects

You may also be interested in related projects focusing on neural scene representations and rendering:

  • Chan et al. pi-GAN. CVPR 2021 (link)
  • Kellnhofer et al. Neural Lumigraph Rendering. CVPR 2021 (link)
  • Lindell et al. Automatic Integration for Fast Neural Rendering. CVPR 2021 (link)
  • Sitzmann et al. MetaSDF. NeurIPS 2020 (link)
  • Sitzmann et al. Scene Representation Networks. NeurIPS 2019 (link)
  • Sitzmann et al. Deep Voxels. CVPR 2019 (link)